LCS

문제 링크

인자를 잘 설정하고 의미에 맞게 풀어야 한다.

발상

주어진 문자열 $S_1$, $S_2$를 교차 비교할 때, 특정 인덱스 $i$, $j$ 에서 문자가 일치한 경우 해당 위치 이전, 즉 $i-1$, $j-1$ 까지의 일치한 경우 수에 +1을 하면 된다. 같은 문자열이 양 문자열에 추가됐기 때문이다. 일치하지 않은 경우는 해당 문자가 한쪽에만 추가될 수 있으므로 $i-1$ 혹은 $j-1$ 중 더 많이 일치한 경우를 고르면 된다. 이 과정을 그림으로 나타내면 아래와 같다. 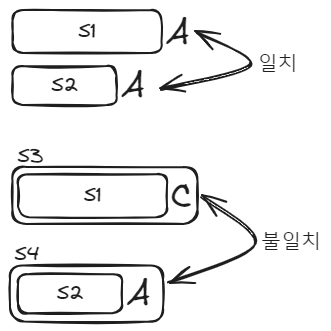일치하는 경우는 일치한 문자를 제외한 S1과 S2의 LCS에 새로 일치한 문자 수 1을 더한 값이 답이 된다. 일치하지 않는 경우는 S3와 S2의 LCS와 S1와 S4의 LCS 중 긴 것이 답이 된다.

점화식

$$\{\begin{array}{l}{n}_{i,j}=\text{i, j 까지 일치한 문자 수}\\ S{1}_i=\text{첫번째 문자열의 i번째 문자}\\ S{2}_j=\text{두번째 문자열의 j번째 문자}\end{array}$$ $$n_{i,j}=\{\begin{array}{ll}{n}_{i-1,j-1}+1& \text{if S1i=S2j}\\ \max (n_{i-1,j},n_{i,j-1})& \text{else}\end{array}$$

예제

아래 예제를 직접 실행해보자. 케이스가 상당히 길어서 이해했다면 굳이 끝까지 보지 않아도 된다.

ACAYKP
CAPCAK

우선 기저 사례로써 두 문자열이 빈 경우가 있다. 이 때 일치하는 문자 수는 당연히 0이다. 또한 문자열 중 어느 하나가 빈 문자열인 경우도 마찬가지로 일치하는 문자 수는 0이다.

S1 = ''
S2 = ''
일치하는 문자 수 = 0

문자가 일치하지 않았으므로 이전 값들 중 큰 것을 고르는데 둘 다 0이므로 일치 수는 0이다.

S1=A
S2=C
일치하는 문자 수 = max(dp('', 'C'), dp('A', '')) = 0

S1=A
S2=CA
일치하는 문자 수 = dp('', 'C') + 1 = 1

S1=A
S2=CAP
일치하는 문자 수 = max(dp('', 'CAP'), dp('A', 'CA')) = 1

S1=A
S2=CAPC
일치하는 문자 수 = max(dp('', 'CAPC'), dp('A', 'CAP')) = 1

S1=A
S2=CAPCA
일치하는 문자 수 = dp('', 'CAPC') + 1 = 1

S1=A
S2=CAPCAK
일치하는 문자 수 = max(dp('', 'CAPCAK'), dp('A', 'CAPCA')) = 1

S1=AC
S2=C
일치하는 문자 수 = dp('A', '') + 1 = 1

S1=AC
S2=CA
일치하는 문자 수 = max(dp('A', 'CA'), dp('AC', 'C')) = 1

S1=AC
S2=CAP
일치하는 문자 수 = max(dp('A', 'CAP'), dp('AC', 'CA')) = 1

S1=AC
S2=CAPC
일치하는 문자 수 = dp('A', 'CAP') + 1 = 2

S1=AC
S2=CAPCA
일치하는 문자 수 = max(dp('A', 'CAPCA'), dp('AC', 'CAPC')) = 2

S1=AC
S2=CAPCAK
일치하는 문자 수 = max(dp('A', 'CAPCAK'), dp('AC', 'CAPCA')) = 2

S1=ACA
S2=C
일치하는 문자 수 = max(dp('AC', 'C'), dp('ACA', '')) = 1

S1=ACA
S2=CA
일치하는 문자 수 = dp('AC', 'C') + 1 = 2

S1=ACA
S2=CAP
일치하는 문자 수 = max(dp('AC', 'CAP'), dp('ACA', 'CA')) = 2

S1=ACA
S2=CAPC
일치하는 문자 수 = max(dp('AC', 'CAPC'), dp('ACA', 'CAP')) = 2

S1=ACA
S2=CAPCA
일치하는 문자 수 = dp('AC', 'CAPC') + 1 = 3

S1=ACA
S2=CAPCAK
일치하는 문자 수 = max(dp('AC', 'CAPCAK'), dp('ACA', 'CAPCA')) = 3

S1=ACAY
S2=C
일치하는 문자 수 = max(dp('ACA', 'C'), dp('ACAY', '')) = 1

S1=ACAY
S2=CA
일치하는 문자 수 = max(dp('ACA', 'CA'), dp('ACAY', 'C')) = 2

S1=ACAY
S2=CAP
일치하는 문자 수 = max(dp('ACA', 'CAP'), dp('ACAY', 'CA')) = 2

S1=ACAY
S2=CAPC
일치하는 문자 수 = max(dp('ACA', 'CAPC'), dp('ACAY', 'CAP')) = 2

S1=ACAY
S2=CAPCA
일치하는 문자 수 = max(dp('ACA', 'CAPCA'), dp('ACAY', 'CAPC')) = 3

S1=ACAY
S2=CAPCAK
일치하는 문자 수 = max(dp('ACA', 'CAPCAK'), dp('ACAY', 'CAPCA')) = 3

S1=ACAYK
S2=C
일치하는 문자 수 = max(dp('ACAY', 'C'), dp('ACAYK', '')) = 1

S1=ACAYK
S2=CA
일치하는 문자 수 = max(dp('ACAY', 'CA'), dp('ACAYK', 'C')) = 2

S1=ACAYK
S2=CAP
일치하는 문자 수 = max(dp('ACAY', 'CAP'), dp('ACAYK', 'CA')) = 2

S1=ACAYK
S2=CAPC
일치하는 문자 수 = max(dp('ACAY', 'CAPC'), dp('ACAYK', 'CAP')) = 2

S1=ACAYK
S2=CAPCA
일치하는 문자 수 = max(dp('ACAY', 'CAPCA'), dp('ACAYK', 'CAPC')) = 3

S1=ACAYK
S2=CAPCAK
일치하는 문자 수 = dp('ACAY', 'CAPCA') + 1 = 4

S1=ACAYKP
S2=C
일치하는 문자 수 = max(dp('ACAYK', 'C'), dp('ACAYKP', '')) = 1

S1=ACAYKP
S2=CA
일치하는 문자 수 = max(dp('ACAYK', 'CA'), dp('ACAYKP', 'C')) = 2

S1=ACAYKP
S2=CAP
일치하는 문자 수 = dp('ACAYK', 'CA') + 1 = 3

S1=ACAYKP
S2=CAPC
일치하는 문자 수 = max(dp('ACAYK', 'CAPC'), dp('ACAYKP', 'CAP')) = 3

S1=ACAYKP
S2=CAPCA
일치하는 문자 수 = max(dp('ACAYK', 'CAPCA'), dp('ACAYKP', 'CAPC')) = 3

S1=ACAYKP
S2=CAPCAK
일치하는 문자 수 = max(dp('ACAYK', 'CAPCAK'), dp('ACAYKP', 'CAPCA')) = 4

코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
int main() {
	string s1, s2; cin >> s1 >> s2;
	int n1 = s1.size(), n2 = s2.size(); vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
	for (int i = 1; i <= n1; i++) {
		for (int j = 1; j <= n2; j++) {
			if (s1[i - 1] == s2[j - 1]) { // 문자가 일치한 경우
				dp[i][j] = dp[i - 1][j - 1] + 1; 
			}
			else {
				dp[i][j] = dp[i - 1][j] > dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1];
			}
		}
	}
	cout << dp[n1][n2];	
	return 0;
}